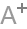
真实世界中的很多系统，包括交通、能源、生物、社会等，都可以由节点和边构成的网络来描述，其中节点表示系统的基本单元，边表示基本单元间的相互作用。这样的简化虽然忽略了系统基本单元本身的性质及在其上发生的动力学过程，但却强调了系统基本单元间的相互作用和系统的组织结构。

尽管不同系统之间存在着固有差别，但是研究表明，很多由不同的真实系统抽象而来的网络都表现出了共同的拓扑性质，而且通过研究网络的拓扑性质可以揭示真实系统的组织原理，形成机制和演化规律等问题。

网络的图论描述

图论是目前复杂网络分析领域最主要的数学工具。在图论中，一个复杂网络可以表述为一个图。图G(V，E)由2个集合构成:节点(vertex或node)集合V和边(edge或link)集合E。节点集合V的大小N表示网络的规模，边集合E的大小M表示网络边的总数。图1给出了一个包含11个节点和18条边的网络示例。

网络中各个节点之间的邻接关系可以由邻接矩阵A来描述。若节点i与节点j相连，即这2个节点是邻居节点，则邻接矩阵元aij= 1;若节点i与j不相连，则aij= 0。这种邻接元为0或1的图称为二值(无权)图。若定义节点i，j之间关系的强弱，即为边赋权值wij，则称为加权图。此外，边无方向的图称为无向图，边有方向的图称为有向图。为简单起见，下面重点介绍无向二值图的拓扑描述。

1.节点度(degree)、度分布(degreedistribution)

度是对节点互相连接统计特性最重要的描述，也反映重要的网络演化特性。度k定义为与节点直接相连的边数。节点的度越大则该节点的连接就越多，节点在网络中的地位也就越重要。度分布P(k)是网络最基本的一个拓扑性质，它表示在网络中等概率随机。

图1一个简单的网络(图)示例

图中圆圈代表网络节点，线段代表节点之间的连接(边)，该网络具有11个节点和18条边，记作G(11，18)。(a)网络G(11，18)中黑色实心节点i有4个邻居节点(灰色实心节点)，且这4个节点之间有3条边(黑色粗实线)相连，故节点i的聚类系数Ci = 3/c(4，2) = 0。5; (b)网络G(11，18)中2个实心节点i，j之间的最短路径长度(黑色粗实线)li，j = 2; (c)网络G(11，18)可以划分为2个模块，黑色实心节点分别为各模块内的区域核心节点(provincial hub)，灰色实心节点为网络中的连接子(connector)

选取的节点度值正好为k的概率，实际分析中一般用网络中度值为k的节点占总节点数的比例近似表示。拥有不同度分布形式的网络在面对网络攻击时会表现出截然不同的网络行为。

2.集群系数(clustering coefficient)

集群系数衡量的是网络的集团化程度，是度量网络的另一个重要参数，表示某一节点i的邻居间互为邻居的可能。节点i的集群系数Ci的值等于该节点邻居间实际连接的边的数目(ei)与可能的最大连接边数(ki(ki–1)/2)的比值(图1(a))，即

网络中所有节点集群系数的平均值为网络的集群系数，即

易知0≤C≤1。由于集群系数只考虑了邻居节点间的直接连接，后来有人提出局部效率(local efficiency)Eloc的概念。任意节点i的局部效率为

其中，Gi指节点i的邻居所构成的子图，ljk表示节点j，k之间的最短路径长度(即边数最少的一条通路)。网络的局部效率为所有节点的局部效率的平均，即